1.【生成模型开山之作】GAN 论文精读
原文连接:Generative Adversarial Netsopen in new window 源码连接:http://www.github.com/goodfeli/adversarialopen in new window
0. 核心总结
本文的核心是通过训练一组生成器-辨别器的对抗网络的思想去得到我们想要的生成网络,本文设计了一个精妙的损失函数和训练算法,使得生成器能最终能收敛到真实数据分布,辨别器能收敛到50%的辨别概率。
1. 摘要
GAN的框架包含两个模型:一个生成模型G和辨别模型D,通过同时训练这两个模型进行对抗, G的目标是通过捕获数据分布来使D犯错的概率最大,而D的目标是估计数据是来自于训练集而不是G。随着对抗训练的完成,G能够恢复训练集的分布且D的分辨概率为50%。
模型G和D都是由神经网络构建,并且通过反向传播来训练。
2. 对抗网络
GAN网络的目标通过数学的表示是:
- 生成模型G:输入一个噪声随机变量pz(z),最优化参数θg,使得模型G(z;θg)能够将输入映射到真实数据x
- 辨别模型D:输入一个数据x,最优化参数θd,输出是真实数据的概率
于是可以构建如下损失函数V(G,D)来对两个参数进行最优化:
GminDmaxV(D,G)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]
根据以下公式,期望的梯度等于原梯度,所以可以使用梯度下降法来进行反向传播:
σ→0lim∇xEϵ∼N(0,σI)f(x+ϵ)=∇xf(x)
下图展示了一个GAN网络对抗训练的过程:
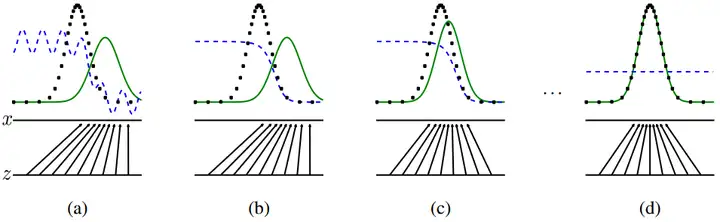 image.png
image.png其中,蓝色虚线表示判别模型的分布D,黑色虚线表示数据真实分布pdata(x),绿色实现表示生成分布pg(x)。两条水平线表示被采样的区域,z是被均匀采样的,向上的箭头表示x=G(z)的映射。
- (a): pg近似pdata,D开始只能部分辨别准确
- (b):在算法内循环中,先最优化训练D,D的最优解为:D∗(x)=pdata(x)+pg(x)pdata(x)
- (c):在训练完D后,D的梯度会引导训练G(z)更接近真实分布
- (d):最终如果训练收敛,则pg(x)=pdata(x),D(X)=21
GAN网络训练算法的伪代码如下:
for iterations do
for k steps do
- 从pz(z)中采样m个minibatch噪声{z(1),…,z(m)}
- 从pdata(x)中采样m个minibatch真实分布{x(1),…,x(m)}
- 通过随机梯度下降算法更新辨别器:
∇θdm1i=1∑m[logD(x(i))+log(1−D(G(z(i))))]
end for
- 从pz(z)中采样m个minibatch噪声{z(1),…,z(m)}
- 通过随机梯度下降算法更新生成器:
∇θgm1i=1∑mlog(1−D(G(z(i))))
end for
梯度下降算法可以使用任意基于梯度的学习算法,本文使用了Momentum。
其中,k为超参数。k的设置很重要,若k较小则辨别器D变化较小导致生成器G也变化较小;若k较大则辨别器D辨别能力很强导致D(G(Z))的梯度接近于0,也影响G的更新。
3. 理论证明
已知我们的目标是使生成数据等于真实数据,辨别器的分辨概率为50%。此节通过理论证明本文设计的损失函数的合理性,为什么通过最优化该损失函数可以收敛至 pg(x)=pdata(x),D(X)=21。
命题1. 对于给定的G,最优的辨别器D是:
DG∗(x)=pdata(x)+pg(x)pdata(x)
证明:辨别器D训练的准则是,对于任意给定的G,令V(G,D)最大。将损失函数展开,得:
V(G,D)=∫xpdata(x)log(D(x))dx+∫zpz(z)log(1−D(G(z)))dz=∫xpdata(x)log(D(x))+pg(x)log(1−D(x))dx
现要求V(G,D)关于D的最大值,则固定G求D的偏导,得:
∂D(x)∂(pdata(x)log(D(x))+pg(x)log(1−D(x)))=D(x)pdata(x)−1−D(x)pg(x)=0,D(x)∈[0,1]⇒D∗(x)=pdata(x)+pg(x)pdata(x)
根据命题1的结果,损失函数可以重新表示为:
C(G)=DmaxV(G,D)=Ex∼pdata[logDG∗(x)]+Ez∼pz[log(1−DG∗(G(z)))]=Ex∼pdata[logDG∗(x)]+Ex∼pg[log(1−DG∗(x))]=Ex∼pdata[logpdata(x)+pg(x)pdata(x)]+Ex∼pg[logpdata(x)+pg(x)pg(x)]
定理1. 当且仅当 pg(x)=pdata(x)时,C(G)达到全局最小值,最小值为−log4。
证明:对C(G)做如下变换:
C(G)=∫xpdata(x)logpdata(x)+pg(x)pdata(x)+pg(x)logpdata(x)+pg(x)pg(x)dx=∫xpdata(x)log2pdata(x)+pg(x)2pdata(x)+pg(x)log2pdata(x)+pg(x)2pg(x)dx=−log4+∫xpdata(x)log2pdata(x)+pg(x)pdata(x)+pg(x)log2pdata(x)+pg(x)pg(x)dx=−log4+KL(pdata∥2pdata+pg)+KL(pg∥2pdata+pg)=−log4+2⋅JS(pdata∥pg)
根据JS散度的非负性,JS(pdata∥pg)≥0,且当且仅当pg=pdata时,JS(pdata∥pg)=0,因此C(G)有最小值−log4。
如果不了解KL和JS散度,可以阅读我的这篇文章:信息量和熵open in new window
定理2. 当G和D有足够容量的时候,且在训练算法中D可以达到其最优解,如果对pg的优化是按照如下公式,那么pg最终可以收敛到 pdata
Ex∼pdata[logDG∗(x)]+Ex∼pg[log(1−DG∗(x))]
证明:把V(G,D)=U(pg,D)看成是一个关于pg的函数,且是凸函数,由于一个凸函数的积分上限函数还是凸函数,所以对凸函数做梯度下降时会得到一个最优解。
实际上,训练算法每次迭代并没有对D优化到极致,只是迭代了k步,但实践中训练算法的表现效果很好。





